

The Standard Model is the name given to the current theory of fundamental particles and how they interact. It makes predictions that can be tested at currently achievable particle energies. It is a successful model, but it includes many arbitrary parameters. It predicts that at higher energies new physics will reveal that these parameters are a necessary part of the model. However, these energies are orders of magnitude away from what is achievable in the foreseeable future.
So what does this have to do with cosmology?
What do we know about the universe today? We know that the universe is expanding.
In the 1920's the famous American astronomer Edwin Hubble made an amazing discovery. He found that, no matter which direction he looked into space, distant galaxies appeared to be moving away from us. The farther away the galaxy is from our galaxy the faster it moves away from us. Hubble was observing the expansion of the Universe.
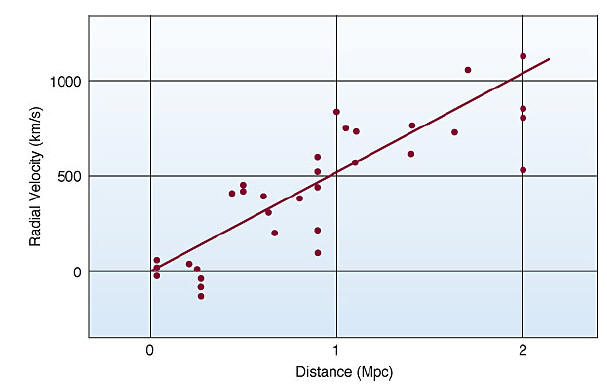
Hubble diagram from 1929 for a few nearby galaxies. Distances are measured in Megaparsecs.
Hubble's law relates the average speed v with which a galaxy retreats from us to the distance R between us and the galaxy.
v = HR
H is the Hubble constant, H ~ 2.5*10-18/s. Hubble's law states that the Universe is expanding.
It may appear that Hubble's law places Earth or our galaxy in a privileged position in the Universe. In fact, just the the opposite is true, as the following one dimensional illustration shows. Imagine a hypothetical Universe that expands by a factor of 2 in a time interval Δt.

In the diagram above, the top line represents the Universe a time interval Δt ago. The different galaxies are identified as A, B, etc, and they are spaced a distance d apart. The middle line represents the Universe now. Since a time interval Δt has gone by, the Universe has doubled in size, every galaxy is now twice as far away from its neighboring galaxy. If we pick galaxy A and measure the distance of each other galaxy from A at t = -Δt and at t = 0 (now), we find that all distances have doubled. A galaxy whose distance from A was n*d at t = -Δt now is a distance 2*n*d away from A. If we calculate the average speed v of the galaxies with respect to A we find v = (2*n*d - n*d)/Δt = n*d/Δt. We find a linear relation between speed and distance. The farther a galaxy is away from any galaxy A, the faster it is moving away from A in an expanding Universe. For a Universe expanding as depicted by the middle line in the above diagram, any observer would see all other galaxies receding with a speed that is directly proportional to distance, which is Hubble's Law.
Hubble's law can be contrasted with a law in which other galaxies retreat from ours all with the same velocity. While the galaxies may be evenly spaced at time -Δt, this is no longer the case at time t = 0, and galaxy A occupies a special point, as the bottom line in the above diagram shows.
In fact, Hubble's law is the unique law for galactic speeds by which no one galaxy occupies a special point within the cosmos. A two-dimensional analogue of the situation described by Hubble's law is provided by dots painted on a spherical balloon. When the balloon is blown up, all the dots recede from each other, with no dot occupying any special position, and a law like Hubble's law holds. If we lived on the surface of such a balloon, any voyage we took would eventually take us back home, and we would conclude that there is no "outside." It has taken centuries of discussion for humankind to understand that it is not at the Universe's physical center. There is no center.
Hubble's law tells us that the universe is expanding. All indicators point to that it has been expanding for 13 - 14 billion years.
The Hubble constant H is constant as a function of position, but not as a function of time, H(r,t) = H(t). Hubble's law can be used to find the time required for galaxies to separate by given amounts. If we assume that H(t) is constant and use Hubble's law to find the time at which all matter was together, that time is infinite.
v = HR, ΔR/Δt = HR, Δt = ΔR/(HR).
The time it takes to get from R = 0 to some R = R0 is found by summing Δt = ΔR/(HR) with ΔR --> 0 from R = 0 to R = R0. This is written as
∫0R0 dR/(HR)
which blows up if we really start at R = 0.
Thus if there was an initial moment when the Universe started to expand, Hubble's law with a constant value of H cannot hold all the way back to that time. We can, however, use the law to make an estimate. If we assume that the recession speed of each galaxy is approximately constant, v = H(t)R states that the expansion time is approximately 13 billion years. Other information, such as theoretical knowledge of stellar evolution and experimental identification of the characteristics of the oldest stars, confirms this estimate to within a factor of 2, and measurements from a satellite-based experiment known as the Wilkinson Microwave Anisotropy Probe (WMAP) allow us to say with one percent accuracy that the Universe is 13.7 billion years old.
Will the Universe expand forever?
Or will the expansion come to a halt? Will the Universe eventually contract again? Which of these outcomes holds depends on whether the gravitational pull of the energy contained in the Universe is strong enough to slow down, and perhaps reverse, the expansion. There is a critical density of energy ρcrit for which the expansion will go on forever, but will slow down and come asymptotically to a stop at infinite time. This critical energy density is given by the formula
ρcrit = 3H2/(8πG),
where H is the Hubble constant and G is Newton's gravitational constant. Less density than this and the expansion goes on forever, more density and the Universe will contract again. This information is often stated in terms of the ratio Ω of the actual density to the critical density. If Ω > 1 the Universe will eventually collapse.
What is the value of Ω? If we look at luminous matter, mainly consisting of the 1011 stars in each of 1011 galaxies, we find Ω = 0.02 - 0.05. However, there is much evidence that dark matter exists, by which we mean matter that does not emit visible light. Estimates of the amount of dark matter can be made in various ways, including the observed rotation profiles of galaxies and the frequency of gravitational lensing, and the conclusion is that there is even more dark matter than luminous matter. Nevertheless, inclusion of dark matter boosts Ω only to 0.2 - 0.3. A value for Ω of 0.3 is a rather unsatisfactory number. In fact, any number other than Ω = 1 presents problems. The Universe is very old, and any random value of Ω > 1 in the early Universe would have the Universe collapse very quickly, or, if Ω < 1, expand much too rapidly to allow for galactic evolution. In fact, calculations show that the only way to have a value of Ω in the vicinity of Ω = 1 today is to have an early-Universe value of Ω equal to one with a precision of one part in 1057. The kind of fine tuning that would be necessary to lead to some value of Ω = 0.3 right now is very unnatural, and it is this kind of thinking that favors Ω exactly equal to one both in the early Universe and therefore also today.
Current thinking about Ω relies on new observations that seem to suggest that the expansion of the Universe, instead of slowing down, is actually accelerating. This can be interpreted as being due to something called dark energy which acts as a form of antigravity. These are new issues, and there are no compelling arguments about what the nature of this dark energy is. With the inclusion of dark energy, it is possible to arrive at Ω = 1.
What else do we know about the universe ? We know that the universe was once very hot.
The Big Bang
In 1946, George Gamow proposed that the primeval fireball, the "big bang," was an intense concentration of pure energy. It is the source of all the matter that now exists in the Universe. The theory predicts that all the galaxies in the Universe should be rushing away from each other at high speeds as a result of that initial big bang. A dictionary definition of the hot big bang theory is "the entire physical Universe, all the matter and energy and even the four dimensions of time and space, burst forth from a state of infinite or near infinite density, temperature, and pressure". It is not as though we are now living in a space in which an explosion once occurred. Rather, space-time itself exploded.
The 1965 observation of the microwave background radiation by Arno Penzias and Robert Wilson convinced most scientists of the validity of the big bang theory. Further observations of the background radiation reported in 1992 have moved the big bang theory from a consensus view to the nearly unanimous view among cosmologists. There was an origin to the Universe approximately 14 billion years ago.
Penzias and Wilson accidentally discovered thie microwave background radiation emanated uniformly from all directions in the sky. The radiation had the characteristic wavelength distribution of an emitter at a temperature of approximately 3 Kelvin (2.73K). The microwave background radiation had in fact been predicted years earlier (1948) by George Gamow, Ralph Alpher, and Robert Herman as a relic of the evolution of the early Universe. Electromagnetic radiation from all regions of the universe that were ~14 billion light years away from our present position at the emission time reaches us now. The radiation was emitted by a gas with a temperature of millions of degree K. But that gas was moving rapidly away from our present position since the universe was expanding. The radiation therefore appears Doppler shifted towards longer wavelength.
Fundamental questions about our Universe remain. What was the Universe like before it was expanding? How did the galaxies and clusters of galaxies that we observe today form? What is most of the matter in the Universe made of?
We are beginning to find answers to some of these questions. The cosmic microwave background radiation plays a key role as it gives us a picture of the Universe as it was only 300000 years after the Big Bang. It turns out to be so remarkably uniform, that it was only in 1992 that the Cosmic Background Explorer (COBE) satellite detected the first non-uniformities in this radiation. There are slight fluctuations in the temperature of the radiation, about one part in a hundred thousand, which are the seeds from which galaxies formed.

| COBE map of temperature fluctuations in the cosmic microwave background. Hotter-than-average regions are shown in red, cooler-than-average regions in blue. The total temperature range shown is ±200 millionths of a Kelvin. |
Two puzzles arose from the dramatic COBE observations. How did the matter in the Universe establish near-perfect equilibrium when distant regions were too far apart to interact? What caused the tiny fluctuations that are essential for the formation of galaxies? Both are answered by a remarkably successful modification of the Hot Big Bang, involving a super-rapid expansion of the very early Universe, called "inflation". This model was developed in the early 1980's, based on the strange properties of the quantum vacuum. Unlike a classical vacuum, the quantum vacuum is not nothingness, but a sea of tiny fluctuations, with an effective "negative pressure". Negative pressure gives rise to extremely fast expansion of the Universe, so that apparently disconnected regions of the Universe were in fact in contact at the beginning of inflation. At the same time as it solves the problem of how equilibrium is established, inflationary expansion also amplifies and ‘unlocks’ the tiny vacuum fluctuations, which eventually become ripples in the density of matter.
Another puzzle arising from observations is the ‘missing matter’ problem. The inflationary model does not have a natural solution to this problem.
From the Big Bang until now, the Universe can be viewed as proceeding through different "epochs" (time periods). In each succeeding epoch the Universe is cooler and less dense. Different interaction and particles dominate each epoch.

How far can we extrapolate into the past to determine what happened?
Current models make predictions starting ~10-43 seconds after the Big Bang. The Planck epoch is time from 0 to 10-43 s. The Standard Model breaks down as quantum cosmologists try to make sense of what the Universe was like at this time. We would need to know how to combine gravity and quantum mechanics before being able to describe what the Universe was like at that time .
When the Universe formed in the Big Bang, it was very hot. In order to understand what occurred during the first few hundred-thousand years of the Universe's history, one must understand what heat is at a microscopic level. Heat is a form of energy. Heat energy is the random kinetic energy of the particles. When particles are very hot, they can behave in ways with which we are unaccustomed. For example, when the electron is very hot it can overcome the force that binds it to the nucleus of an atom, and it will become a free electron. The temperature at which that happens is approximately 3000 K. At temperatures above 3000 K atoms do not exist. The temperature of the Universe was approximately 1032 K when it was 10-43 s old. From this time on the Standard Model can be used to make predictions about the particles present and their interactions.
Particle physics, by its very nature, is concerned with the smallest scales known, currently about 10-18 m. At the opposite extreme is astrophysics and cosmology, the study of the structure and origin of the whole Universe, whose size is of order 1026 m. Paradoxically, these two extreme branches have been growing increasingly dependent on one another for many years. Astronomers studying stellar spectra have needed to understand and have contributed to atomic physics for more than a century. A proper understanding of the energy source and evolution of stars came only after the development of nuclear physics in the 1930s. Most recently, it has become apparent that during the first moments after the big bang, the whole Universe was a natural laboratory for elementary-particle physics. For the first 3 minutes the temperature was so high that no atoms or nuclei could exist, and the Universe was a fiery gas of leptons and hadrons. During the first microsecond or so, the temperature may have been high enough that hadrons could not exist and there were only leptons and quarks. One of the motivations for building particle accelerators with higher and higher energies is to allow physicists to observe collisions that approximate conditions in these earliest moments of the Universe. Because the first moments of the Universe presumably determined its subsequent evolution, an understanding of elementary particles has become very important to astrophysics, and recent years have witnessed several papers in astrophysics published by particle theorists and vice versa.
Examples: